A 7.93 kg box is pulled along a horizontal surface by a force 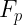 of 84.0 N applied at a
of 84.0 N applied at a 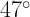 angle. If the coefficient of kinetic friction is 0.35, what is the acceleration of the box?
angle. If the coefficient of kinetic friction is 0.35, what is the acceleration of the box?
SOLUTION:
The free-body diagram of the box

Solve for the normal force
Solve for the friction force
Solve for the acceleration in the horizontal direction
Therefore, the acceleration of the box is 6.51 m/s2 along the horizontal surface.


You must be logged in to post a comment.