Category Archives: Engineering Mathematics Blog

The formula states that we need to get the sum of $\displaystyle \left(x_i-\overline{x}\right)^2$ , so we can use a table to solve $\displaystyle \left(x_i-\overline{x}\right)^2$ for every sample.

Note: You can refer to the solution of Exercise 1.7 on how to use a table to solve for the variance.

The variance is

$\displaystyle \left(s^2\right)_A=\sum _{i=1}^{10}\:\frac{\left(x_i-7.950\right)^2}{10-1}$

$\displaystyle =1.2078$

The standard deviation is just the square root of the variance. That is

$\displaystyle s_A=\sqrt{1.2078}=1.099$

For Company B:

Using the same method employed for Company A, we can show that the variance and standard deviation for the samples in Company B are

$\displaystyle \left(s^2\right)_B=0.3249$ and $\displaystyle s_B=0.570$ .

Arizona State University| PHY 121: Univ Physics I: Mechanics|Homework 1-1| Problem 2

Learning Goal:

To practice Tactics Box 1.2 Vector Subtraction.

Vector subtraction has some similarities to the subtraction of two scalar quantities. With numbers, subtraction is the same as the addition of a negative number. For example, 5−3 is the same as 5+(−3). Similarly, A⃗ −B⃗ =A⃗ +(−B⃗ ). We can use the rules for vector addition and the fact that −B⃗ is a vector opposite in direction to B⃗ to form rules for vector subtraction, as explained in this tactics box.

The figure shows two vectors. Vector A is on the left and is directed upwards to the right. Vector B is on the right and is directed downwards to the right.

To subtract B⃗ from A⃗ (Figure 1), perform these steps:

Draw A⃗ .
Draw −B⃗ and place its tail at the tip of A⃗ .
Draw an arrow from the tail of A⃗ to the tip of −B⃗ . This is vector A⃗ −B⃗ .

Part A

Draw vector C⃗ =A⃗ −B⃗ by following the steps in the tactics box above. When drawing −B⃗ , keep in mind that it has the same magnitude as B⃗ but opposite direction.

Part B

Draw vector F⃗ =D⃗ −E⃗ by following the steps in the tactics box above. When drawing −E⃗ , keep in mind that it has the same magnitude as E⃗ but opposite direction.

ANSWERS:

Part A

Part B

Arizona State University| PHY 121: Univ Physics I: Mechanics|Homework 1-1| Problem 1

Learning Goal:
To practice Tactics Box 1.1 Vector Addition.

Vector addition obeys rules that are different from those for the addition of two scalar quantities. When you add two vectors, their directions, as well as their magnitudes, must be taken into account. This Tactics Box explains how to add vectors graphically.

To add B⃗ to A⃗ (Figure 1), perform these steps:

Draw A⃗ .
Place the tail of B⃗ at the tip of A⃗ .
Draw an arrow from the tail of A⃗ to the tip of B⃗ . This is vector A⃗ +B⃗ .

Part A

Create the vector R⃗ =A⃗ +B⃗ by following the steps in the Tactics Box above. When moving vector B⃗ , keep in mind that its direction should remain unchanged.

Part B

Create the vector R⃗ =C⃗ +D⃗ by following the steps in the Tactics Box above. When moving vector D⃗ , keep in mind that its direction should remain unchanged. The location, orientation, and length of your vectors will be graded.

ANSWERS:

Part A

Part B

Help

Engineering-Math.org offers a range of academic services to help you achieve the results you’re after. We offer live online tutoring, PDF textbooks, online course help, project assistance, thesis and capstone project assistance, homework help, or even exams.

Please be assured that all information and transactions will be held with utmost confidentiality.

Let’s work on your success.

Send us a message now!

Which service/product do you need?

PDF Textbooks

Online Tutoring

Homework or Assignments

PDF Solution Manuals

For other concerns, please send your queries to any of the following:

Email: help@engineering-math.org

WhatsApp: +639178611702

Grantham PHY220 Week 2 Assignment Problem 8

If a car is traveling at 50 m/s and then stops over 300 meters (while sliding), what is the coefficient of kinetic friction between the tires of the car and the road?

SOLUTION:

Draw the free-body diagram of the car

Consider the vertical direction

$\sum F_y=ma_y$

$F_N-mg=0$

$F_N=mg$

Consider the motion in the horizontal direction

Solve for the acceleration of the car.

$v^2=\left(v_0\right)^2+2a_x\Delta x$

$a_x=\frac{v^2-\left(v_0\right)^2}{2\Delta x}=\frac{0-50^2}{2\left(300\right)}=-4.17\:m/s^2$

Solve for the coefficient of kinetic friction

$\sum F_x=ma_x$

$-F_{fr}=ma_x$

$-\mu _kF_N=ma_x$

$\mu _k=\frac{ma_x}{-F_N}=\frac{m\:\left(-4.17\right)}{-m\left(9.80\right)}=\frac{4.17}{9.80}$

$\mu _k=0.43$

Grantham PHY220 Week 2 Assignment Problem 7

A 7.93 kg box is pulled along a horizontal surface by a force 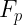$F_p$ of 84.0 N applied at a 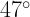$47^{\circ}$ angle. If the coefficient of kinetic friction is 0.35, what is the acceleration of the box?

SOLUTION:

The free-body diagram of the box

week 2 problem 7

Solve for the normal force

$\sum F_y=ma_y$

$F_N-mg+F_psin\left(47.0^{\circ} \right)=0$

$F_N-7.93\left(9.80\right)+84.0\:sin\left(47^{\circ} \right)=0$

$F_N=16.28\:N$

Solve for the friction force

$F_{fr}=\mu _kF_N=0.35\left(16.28\:N\right)=5.70\:N$

Solve for the acceleration in the horizontal direction

$\sum F_x=ma_x$

$F_p\:cos\:\left(47^{\circ} \right)-F_{fr}=7.93\left(a_x\right)$

$84.0\:N\cdot cos\:\left(47^{\circ} \right)-5.70\:N=7.93\:kg\:\cdot \left(a_x\right)$

$a_x=\frac{51.59\:N}{7.93\:kg}=6.51\:m/s^2$

Therefore, the acceleration of the box is 6.51 m/s² along the horizontal surface.

Grantham PHY220 Week 2 Assignment Problem 6

If the acceleration due to gravity on the Moon is 1/6 that what is on the Earth, what would a 100 kg man weight on the Moon? If a person tried to simulate this gravity in an elevator, how fast would it have to accelerate and in which direction?

SOLUTION:

The acceleration due to gravity on the moon is

$g_m=\frac{1}{6}\left(9.80\:m/s^2\right)=1.63\:m/s^2$

The weight of a 100-kg man on the moon is

$W_m=mg_m=\left(100\:kg\right)\left(1.63\:m/s^2\right)=163.3\:N$

If the elevator is accelerating upward then the acceleration would be greater. The person would be pushed toward the ﬂoor of the elevator making the weight increase. Therefore, the elevator must be going down to decrease the acceleration.

For a 100 kg man to experience a 163.3 N in an elevator,

$F=ma$

$163.3\:N=100\:kg\:\left(9.80\:m/s^2-a_e\right)$

$9.80-a_e=\frac{163.3}{100}$

$a_e=9.80-\frac{163.3}{100}$

$a_e=8.167\:m/s^2$

Therefore, the elevator should be accelerated at 8.167 m/s² downward for a 100-kg man to simulate his weight just like his weight in the moon which has 1/6 of the Earth’s gravity acceleration.

Grantham PHY220 Week 2 Assignment Problem 5

If a 1500 kg car stopped from an in 5.6 seconds with an applied force of 5000 N, how fast was it initially traveling?

Solution:

There is a negative acceleration since the car decelerates.

$F=ma$

$a=\frac{F}{m}=\frac{5000\:N}{1500\:kg}=-3.33\:m/s^2$

$v=v_0+at$

$v_0=v-at$

$v_0=0-\left(-3.33\:m/s^2\right)\left(5.6\:s\right)$

$v_0=18.6\:m/s$

The car was initially traveling at $18.6\:m/s$ .

Grantham PHY220 Week 2 Assignment Problem 4

A not so brilliant physics student wants to jump from a 3rd-floor apartment window to the swimming pool below. The problem is the base of the apartment is 8.00 meters from the pool’s edge. If the window is 20.0 meters high, how fast does the student have to be running horizontally to make it to the pool’s edge?

Solution:

Since the student will be running horizontally, there is no initial vertical velocity, $v_{0_y}=0$ . We are also given $\Delta x=8\:m$ , and $\Delta y=-20\:m$ .

Consider the vertical component of the motion.

$\Delta y=v_{0_y}t-\frac{1}{2}gt^2$

$-20=0-\frac{1}{2}\left(9.80\right)t^2$

$-20=-4.9t^2$

$t^2=\frac{20}{4.9}$

$t=\sqrt{\frac{20}{4.9}}$

$t=2.02\:s$

Consider the horizontal component of the motion

$\Delta x=v_{0_x}t$

$v_{0_x}=\frac{\Delta x}{t}$

$v_{0_x}=\frac{8}{2.02}$

$v_{0_x}=3.96\:m/s$

Therefore, the student should be running 3.96 m/s horizontally to make it to the pool’s edge.

Engineering Mathematics and Sciences

Your virtual study buddy in Mathematics, Engineering Sciences, and Civil Engineering

Category Archives: Engineering Mathematics Blog

Mechanics of Materials: An Integrated Learning System 4th Edition by Timothy A. Philpot Complete Solution Manual

Mean and Variance | Introduction to Statistics and Data Analysis | Probability & Statistics for Engineers & Scientists | Walpole | Problem 1.10

For the data of Exercise 1.4 on page 13, compute both the mean and variance in “flexibility” for both company A and company B.

Solution:

Arizona State University| PHY 121: Univ Physics I: Mechanics|Homework 1-1| Problem 2

Arizona State University| PHY 121: Univ Physics I: Mechanics|Homework 1-1| Problem 1

Help

Let’s work on your success.

Which service/product do you need?

Grantham PHY220 Week 2 Assignment Problem 8

If a car is traveling at 50 m/s and then stops over 300 meters (while sliding), what is the coefficient of kinetic friction between the tires of the car and the road?

Grantham PHY220 Week 2 Assignment Problem 7

A 7.93 kg box is pulled along a horizontal surface by a force $F_p$ of 84.0 N applied at a $47^{\circ}$ angle. If the coefficient of kinetic friction is 0.35, what is the acceleration of the box?

Grantham PHY220 Week 2 Assignment Problem 6

If the acceleration due to gravity on the Moon is 1/6 that what is on the Earth, what would a 100 kg man weight on the Moon? If a person tried to simulate this gravity in an elevator, how fast would it have to accelerate and in which direction?

Grantham PHY220 Week 2 Assignment Problem 5

If a 1500 kg car stopped from an in 5.6 seconds with an applied force of 5000 N, how fast was it initially traveling?

Grantham PHY220 Week 2 Assignment Problem 4

For the data of Exercise 1.4 on page 13, compute both the mean and variance in “flexibility” for both company A and company B.

Solution:

Let’s work on your success.

Which service/product do you need?

If a car is traveling at 50 m/s and then stops over 300 meters (while sliding), what is the coefficient of kinetic friction between the tires of the car and the road?

A 7.93 kg box is pulled along a horizontal surface by a force of 84.0 N applied at a angle. If the coefficient of kinetic friction is 0.35, what is the acceleration of the box?

If the acceleration due to gravity on the Moon is 1/6 that what is on the Earth, what would a 100 kg man weight on the Moon? If a person tried to simulate this gravity in an elevator, how fast would it have to accelerate and in which direction?

If a 1500 kg car stopped from an in 5.6 seconds with an applied force of 5000 N, how fast was it initially traveling?

A 7.93 kg box is pulled along a horizontal surface by a force $F_p$ of 84.0 N applied at a $47^{\circ}$ angle. If the coefficient of kinetic friction is 0.35, what is the acceleration of the box?